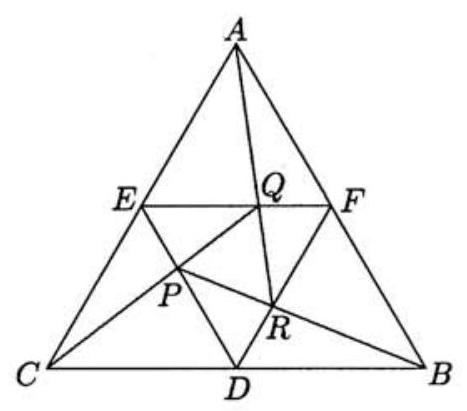
Let A B C be equilateral, and D, E, and F be the midpoints of \overline{B C}, \overline{C A}, and \overline{A B}, respectively. There exist points P, Q, and R on \overline{D E}, \overline{E F}, and \overline{F D}, respectively, with the property that P is on \overline{C Q}, Q is on \overline{A R}, and R is on \overline{B P}. The ratio of the area of triangle A B C to the area of triangle P Q R is a+b \sqrt{c}, where a, b, and c are integers, and c is not divisible by the square of any prime. What is a^{2}+b^{2}+c^{2} ?