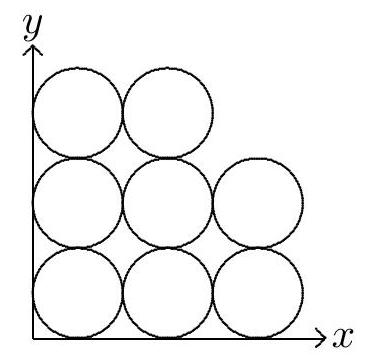
Eight circles of diameter 1 are packed in the first quadrant of the coordinate plane as shown. Let region \mathcal{R} be the union of the eight circular regions. Line \ell, with slope 3 , divides \mathcal{R} into two regions of equal area. Line \ell 's equation can be expressed in the form a x=b y+c, where a, b, and c are positive integers whose greatest common divisor is 1 . Find a^{2}+b^{2}+c^{2}.