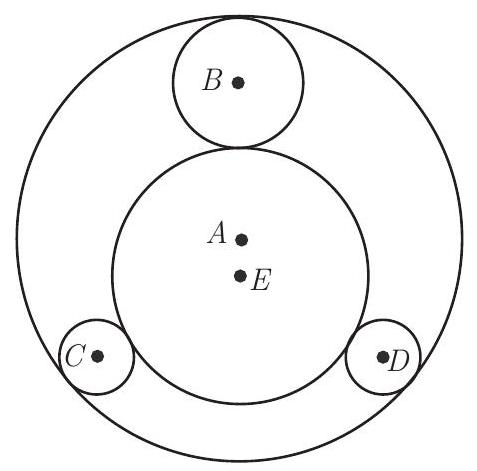
Equilateral triangle T is inscribed in circle A, which has radius 10 . Circle B with radius 3 is internally tangent to circle A at one vertex of T. Circles C and D, both with radius 2 , are internally tangent to circle A at the other two vertices of T. Circles B, C, and D are all externally tangent to circle E, which has radius \frac{m}{n}, where m and n are relatively prime positive integers.
Find m+n.