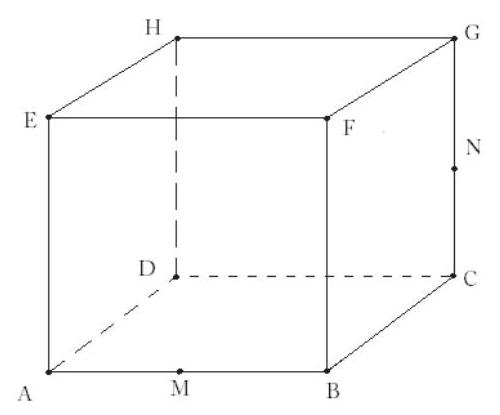
Cube A B C D E F G H, labeled as shown below, has edge length 1 and is cut by a plane passing through vertex D and the midpoints M and N of \overline{A B} and \overline{C G}, respectively. The plane divides the cube into two solids. The volume of the larger of the two solids can be written in the form \frac{p}{q}, where p and q are relatively prime positive integers. Find p+q.