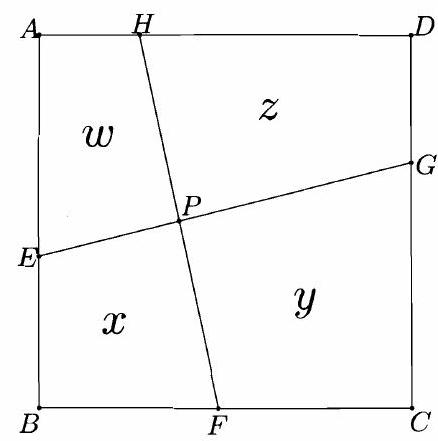
On square A B C D, points E, F, G, and H lie on sides \overline{A B}, \overline{B C}, \overline{C D}, and \overline{D A}, respectively, so that \overline{E G} \perp \overline{F H} and E G=F H=34. Segments \overline{E G} and \overline{F H} intersect at a point P, and the areas of quadrilaterals A E P H, B F P E, C G P F, and D H P G are in the ratio 269:275:405:411. Find the area of square A B C D.