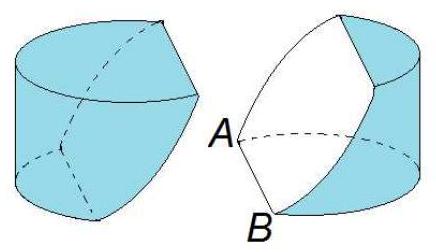
A block of wood has the shape of a right circular cylinder with radius 6 and height 8 , and its entire surface has been painted blue. Points A and B are chosen on the edge of one of the circular faces of the cylinder so that \overparen{A B} on that face measures 120^{\circ}. The block is then sliced in half along the plane that passes through point A, point B, and the center of the cylinder, revealing a flat, unpainted face on each half. The area of one of these unpainted faces is a \cdot \pi+b \sqrt{c}, where a, b, and c are integers and c is not divisible by the square of any prime. Find a+b+c.