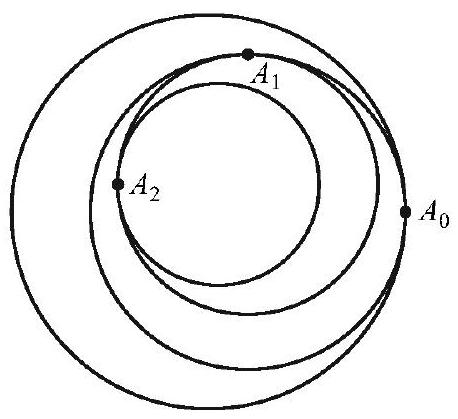
Circle C_{0} has radius 1 , and the point A_{0} is a point on the circle. Circle C_{1} has radius r<1 and is internally tangent to C_{0} at point A_{0}. Point A_{1} lies on circle C_{1} so that A_{1} is located 90^{\circ} counterclockwise from A_{0} on C_{1}. Circle C_{2} has radius r^{2} and is internally tangent to C_{1} at point A_{1}. In this way a sequence of circles C_{1}, C_{2}, C_{3}, \ldots and a sequence of points on the circles A_{1}, A_{2}, A_{3}, \ldots are constructed, where circle C_{n} has radius r^{n} and is internally tangent to circle C_{n-1} at point A_{n-1}, and point A_{n} lies on C_{n} 90^{\circ} counterclockwise from point A_{n-1}, as shown in the figure below. There is one point B inside all of these circles. When r=\frac{11}{60}, the distance from the center of C_{0} to B is \frac{m}{n}, where m and n are relatively prime positive integers. Find m+n.