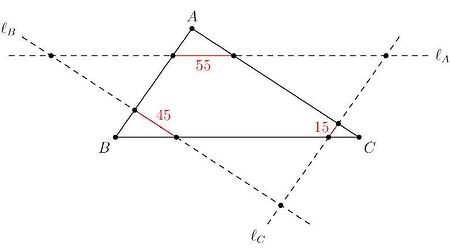
Triangle A B C has side lengths A B=120, B C=220, and A C=180. Lines \ell_{A}, \ell_{B}, and \ell_{C} are drawn parallel to \overline{B C}, \overline{A C}, and \overline{A B}, respectively, such that the intersection of \ell_{A}, \ell_{B}, and \ell_{C} with the interior of \triangle A B C are segments of length 55,45 , and 15 , respectively. Find the perimeter of the triangle whose sides lie on \ell_{A}, \ell_{B}, and \ell_{C}.