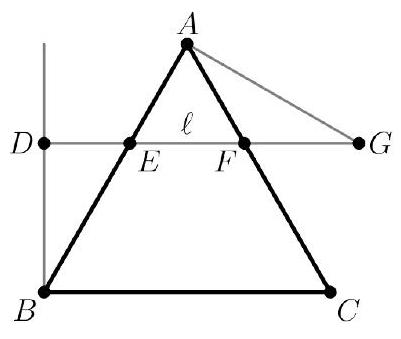
Equilateral triangle A B C has side length 840 . Point D lies on the same side of line B C as A such that \small\overline{B D} \perp \overline{B C}. The line \ell through D parallel to line B C intersects sides \small\overline{A B} and \small\overline{A C} at points E and F, respectively. Point G lies on \ell such that F is between E and G, \triangle A F G is isosceles, and the ratio of the area of \triangle A F G to the area of \triangle B E D is 8: 9. Find A F.