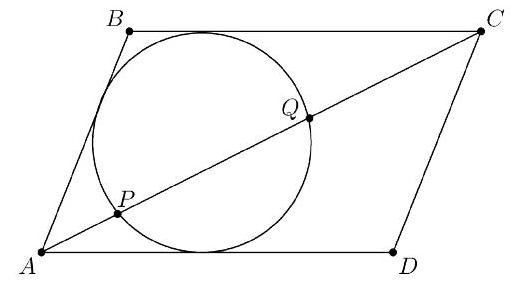
Let A B C D be a parallelogram with \angle B A D<90^{\circ}. A circle tangent to sides \overline{D A}, \overline{A B}, and \overline{B C} intersects diagonal \overline{A C} at points P and Q with A P<A Q, as shown. Suppose that A P=3, P Q=9, and Q C=16. Then the area of A B C D can be expressed in the form m \sqrt{n}, where m and n are positive integers, and n is not divisible by the square of any prime. Find m+n.