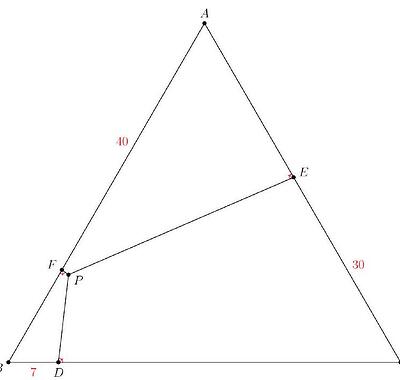
Let \triangle A B C be an equilateral triangle with side length 55 . Points D, E, and F lie on \overline{B C}, \overline{C A}, and \overline{A B}, respectively, with B D=7, C E=30, and A F=40. Point P inside \triangle A B C has the property that
\angle A E P=\angle B F P=\angle C D P
Find \tan ^{2}(\angle A E P).