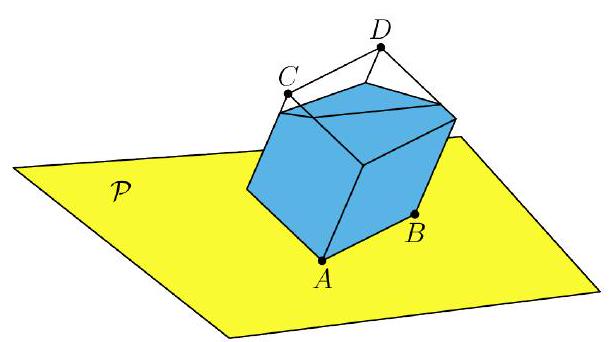
A cube-shaped container has vertices A, B, C, and D, where \overline{A B} and \overline{C D} are parallel edges of the cube, and \overline{A C} and \overline{B D} are diagonals of faces of the cube, as shown. Vertex A of the cube is set on a horizontal plane \mathcal{P} so that the plane of the rectangle A B D C is perpendicular to \mathcal{P}, vertex B is 2 meters above \mathcal{P}, vertex C is 8 meters above \mathcal{P}, and vertex D is 10 meters above \mathcal{P}. The cube contains water whose surface is parallel to \mathcal{P} at a height of 7 meters above \mathcal{P}. The volume of water is \frac{m}{n} cubic meters, where m and n are relatively prime positive intgers. Find m+n.