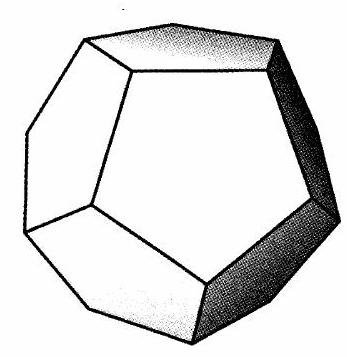
As shown in the figure below, a regular dodecahedron (the polyhedron consisting of 12 congruent regular pentagonal faces) floats in space with two horizontal faces. Note that there is a ring of five slanted faces adjacent to the top face, and a ring of five slanted faces adjacent to the bottom face. How many ways are there to move from the top face to the bottom face via a sequence of adjacent faces so that each face is visited at most once and moves are not permitted from the bottom ring to the top ring?
Answer Choices
A. 125
B. 250
C. 405
D. 640
E. 810