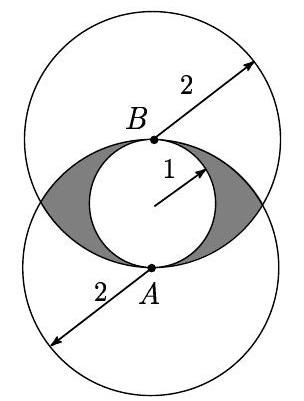
A circle of radius 1 is internally tangent to two circles of radius 2 at points A and B, where A B is a diameter of the smaller circle. What is the area of the region, shaded in the gure, that is outside the smaller circle and inside each of the two larger circles?
Answer Choices
A. \dfrac{5}{3} \pi - 3 \sqrt{2}
B. \dfrac{5}{3}\pi-2 \sqrt{3}
C. \dfrac{8}{3} \pi - 3 \sqrt{3}
D. \dfrac{8}{3} \pi - 3 \sqrt{2}
E. \dfrac{8}{3} \pi - 2 \sqrt{3}