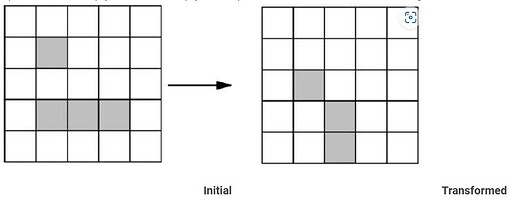
Each square in a 5 \times 5 grid is either filled or empty, and has up to eight adjacent neighboring squares, where neighboring squares share either a side or a corner. The grid is transformed by the following rules:
Any filled square with two or three filled neighbors remains filled.
Any empty square with exactly three filled neighbors becomes a filled square.
All other squares remain empty or become empty.
A sample transformation is shown in the figure below.
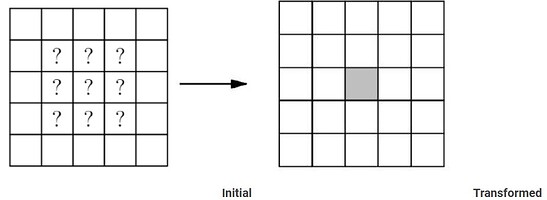
Suppose the 5 \times 5 grid has a border of empty squares surrounding a 3 \times 3 subgrid. How many initial configurations will lead to a transformed grid consisting of a single filled square in the center after a single transformation? (Rotations and reflections of the same configuration are considered different.)
Answer Choices
A. 14
B. 18
C. 22
D. 26
E. 30