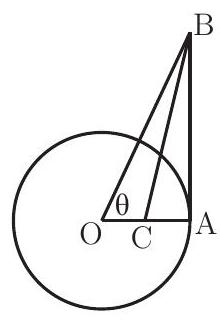
A circle centered at O has radius 1 and contains the point A. Segment A B is tangent to the circle at A and \angle A O B=\theta. If point C lies on \overline{O A} and \overline{B C} bisects \angle A B O, then O C=
Answer Choices
A. \sec ^{2} \theta-\tan \theta
B. \dfrac{1}{2}
C. \dfrac{\cos ^{2} \theta}{1+\sin \theta}
D. \dfrac{1}{1+\sin \theta}
E. \dfrac{\sin \theta}{\cos ^{2} \theta}