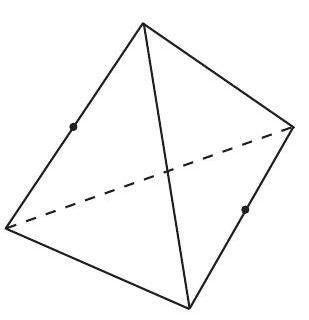
An insect lives on the surface of a regular tetrahedron with edges of length 1 . It wishes to travel on the surface of the tetrahedron from the midpoint of one edge to the midpoint of the opposite edge. What is the length of the shortest such trip? (Note: Two edges of a tetrahedron are opposite if they have no common endpoint.)
Answer Choices
A. \dfrac{1}{2} \sqrt{3}
B. 1
C. \sqrt{2}
D. \dfrac{3}{2}
E. 2