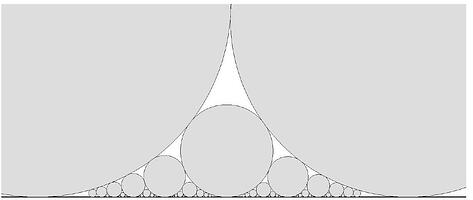
A collection of circles in the upper half-plane, all tangent to the x-axis, is constructed in layers as follows. Layer L_{0} consists of two circles of radii 70^{2} and 73^{2} that are externally tangent. For k \geq 1, the circles in \bigcup_{j=0}^{k-1} L_{j} are ordered according to their points of tangency with the x-axis. For every pair of consecutive circles in this order, a new circle is constructed externally tangent to each of the two circles in the pair. Laver L_{k} consists of the 2^{k-1} circles constructed in this way. Let S=\bigcup_{j=0}^{6} L_{j}, and for every circle C denote by r(C) its radius. What is
\sum_{C \in S} \dfrac{1}{\sqrt{r(C)}} ?
Answer Choices
A. \dfrac{286}{35}
B. \dfrac{583}{70}
C. \dfrac{715}{73}
D. \dfrac{143}{14}
E. \dfrac{1573}{146}