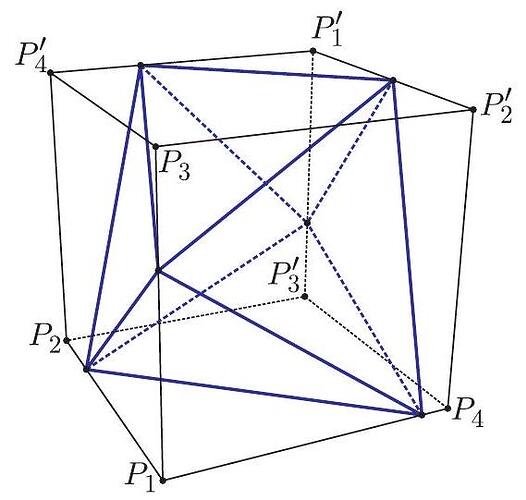
A unit cube has vertices P_{1}, P_{2}, P_{3}, P_{4}, P_{1}^{\prime}, P_{2}^{\prime}, P_{3}^{\prime}, and P_{4}^{\prime}. Vertices P_{2}, P_{3}, and P_{4} are adjacent to P_{1}, and for 1 \leq i \leq 4, vertices P_{i} and P_{i}^{\prime} are opposite to each other. A regular octahedron has one vertex in each of the segments P_{1} P_{2}, P_{1} P_{3}, P_{1} P_{4}, P_{1}^{\prime} P_{2}^{\prime}, P_{1}^{\prime} P_{3}^{\prime}, and P_{1}^{\prime} P_{4}^{\prime}. What is the octahedron’s side length?
Answer Choices
A. \dfrac{3 \sqrt{2}}{4}
B. \dfrac{7 \sqrt{6}}{16}
C. \dfrac{\sqrt{5}}{2}
D. \dfrac{2 \sqrt{3}}{3}
E. \dfrac{\sqrt{6}}{2}