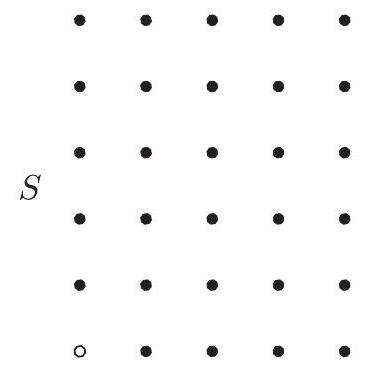
Let S=\{(x, y): x \in\{0,1,2,3,4\}, y \in\{0,1,2,3,4,5\}, and (x, y) \neq(0,0)\}. Let T be the set of all right triangles whose vertices are in S. For every right triangle t=\triangle A B C with vertices A, B, and C in counter-clockwise order and right angle at A, let f(t)=\tan (\angle C B A). What is
\prod_{t \in T} f(t) ?
Answer Choices
A. 1
B. \dfrac{625}{144}
C. \dfrac{125}{24}
D. 6
E. \dfrac{625}{24}