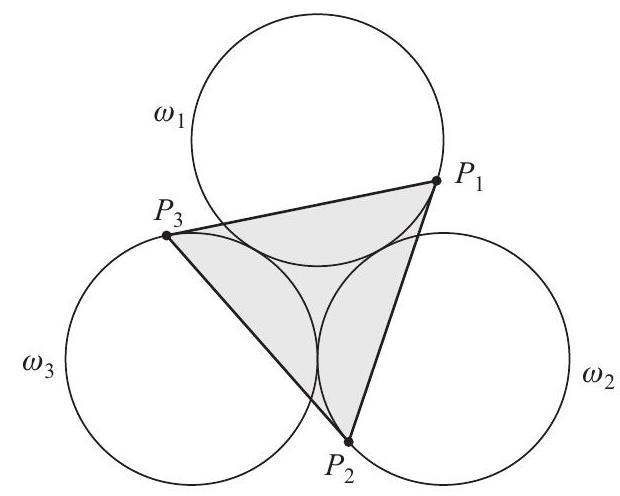
Circles \omega_{1}, \omega_{2}, and \omega_{3} each have radius 4 and are placed in the plane so that each circle is externally tangent to the other two. Points P_{1}, P_{2}, and P_{3} lie on \omega_{1}, \omega_{2}, and \omega_{3}, respectively, so that P_{1} P_{2}=P_{2} P_{3}= P_{3} P_{1} and line P_{i} P_{i+1} is tangent to \omega_{i} for each i=1,2,3, where P_{4}=P_{1}. See the figure below. The area of \triangle P_{1} P_{2} P_{3} can be written in the form \sqrt{a}+\sqrt{b}, where a and b are positive integers. What is a+b ?
Answer Choices
A. 546
B. 548
C. 550
D. 552
E. 554