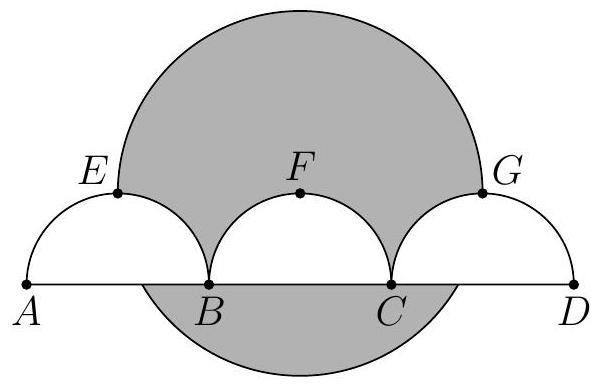
As shown in the figure, line segment \overline{A D} is trisected by points B and C so that
A B=B C=C D=2.
Three semicircles of radius 1, \widehat{AEB}, \widehat{BFC}, and \widehat{CGD}, have their diameters on \overline{A D}, and are tangent to line E G at E, F, and G, respectively. A circle of radius 2 has its center on F. The area of the region inside the circle but outside the three semicircles, shaded in the figure, can be expressed in the form
\dfrac{a}{b} \cdot \pi-\sqrt{c}+d
where a, b, c, and d are positive integers and a and b are relatively prime. What is a+b+c+d ?
Answer Choices
A. 13
B. 14
C. 15
D. 16
E. 17