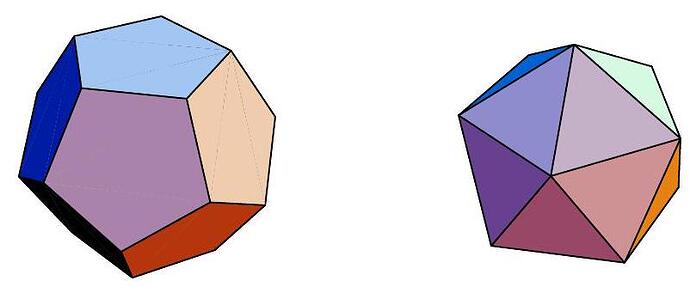
Let D be a dodecahedron which can be inscribed in a sphere with radius R. Let I be an icosahedron which can also be inscribed in a sphere of radius R. Which has the greater volume, and why?
Note: A regular polyhedron is a geometric solid, all of whose faces are congruent regular polygons, in which the same number of polygons meet at each vertex. A regular dodecahedron is a polyhedron with 12 faces which are regular pentagons and a regular icosahedron is a polyhedron with 20 faces which are equilateral triangles. A polyhedron is inscribed in a sphere if all of its vertices lie on the surface of the sphere.
The illustration below shows a dodecahdron and an icosahedron, not necessarily to scale.