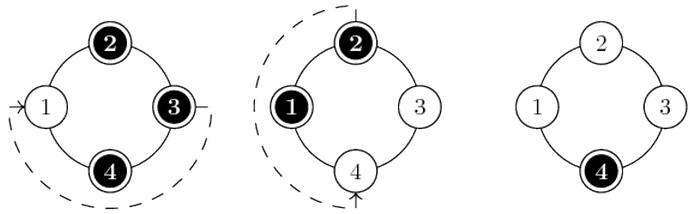
There are n holes in a circle. The holes are numbered 1,2,3 and so on to n. In the beginning, there is a peg in every hole except for hole 1. A peg can jump in either direction over one adjacent peg to an empty hole immediately on the other side. After a peg moves, the peg it jumped over is removed. The puzzle will be solved if all pegs disappear except for one. For example, if n=4 the puzzle can be solved in two jumps: peg 3 jumps peg 4 to hole 1 , then peg 2 jumps the peg in 1 to hole 4 . (See illustration below, in which black circles indicate pegs and white circles are holes.)
(a) Can the puzzle be solved when n=5 ?
(b) Can the puzzle be solved when n=2014 ?
In each part (a) and (b) either describe a sequence of moves to solve the puzzle or explain why it is impossible to solve the puzzle.