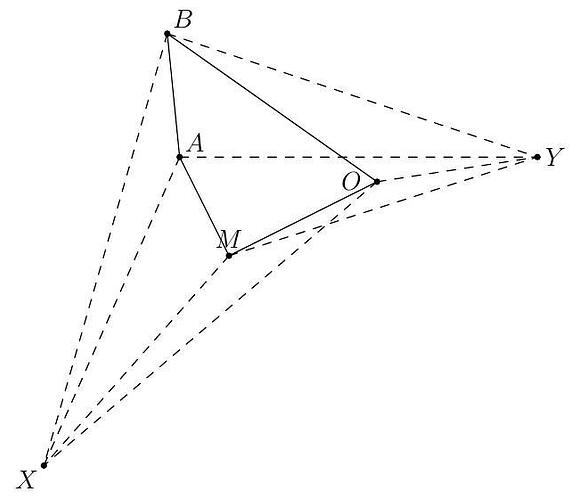
The corners of a fixed convex (but not necessarily regular) n-gon are labeled with distinct letters. If an observer stands at a point in the plane of the polygon, but outside the polygon, they see the letters in some order from left to right, and they spell a “word” (that is, a string of letters; it doesn’t need to be a word in any language). For example, in the diagram below (where n=4 ), an observer at point X would read “BAMO,” while an observer at point Y would read “MOAB.”
Determine, as a formula in terms of n, the maximum number of distinct n-letter words which may be read in this manner from a single n-gon. Do not count words in which some letter is missing because it is directly behind another letter from the viewer’s position.