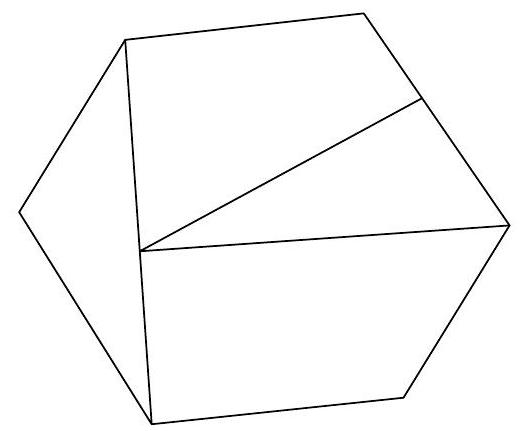
To dissect a polygon means to divide it into several regions by cutting along finitely many line segments. For example, the diagram below shows a dissection of a hexagon into two triangles and two quadrilaterals:
An integer-ratio right triangle is a right triangle whose side lengths are in an integer ratio. For example, a triangle with sides 3,4,5 is an integer-ratio right triangle, and so is a triangle with sides \frac{5}{2} \sqrt{3}, 6 \sqrt{3}, \frac{13}{2} \sqrt{3}. On the other hand, the right triangle with sides \sqrt{2}, \sqrt{5}, \sqrt{7} is not an integer-ratio right triangle.
Determine, with proof, all integers n for which it is possible to completely dissect a regular n-sided polygon into integer-ratio right triangles.