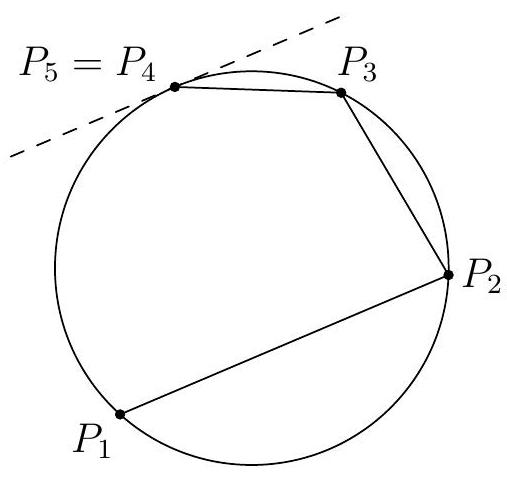
Let points P_{1}, P_{2}, P_{3}, and P_{4} be arranged around a circle in that order. (One possible example is drawn in Diagram 1.) Next draw a line through P_{4} parallel to \overline{P_{1} P_{2}}, intersecting the circle again at P_{5}. (If the line happens to be tangent to the circle, we simply take P_{5}=P_{4}, as in Diagram 2. In other words, we consider the second intersection to be the point of tangency again.) Repeat this process twice more, drawing a line through P_{5} parallel to \overline{P_{2} P_{3}}, intersecting the circle again at P_{6}, and finally drawing a line through P_{6} parallel to \overline{P_{3} P_{4}}, intersecting the circle again at P_{7}. Prove that P_{7} is the same point as P_{1}.
Diagram 1
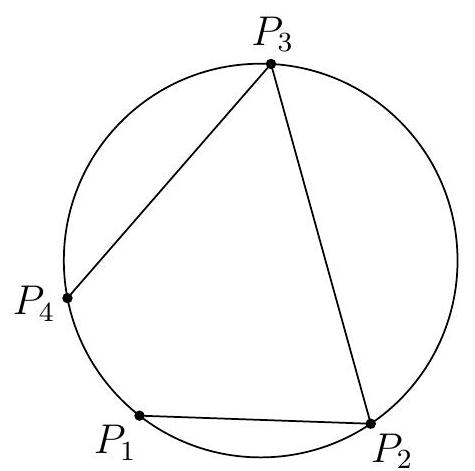
Diagram 2