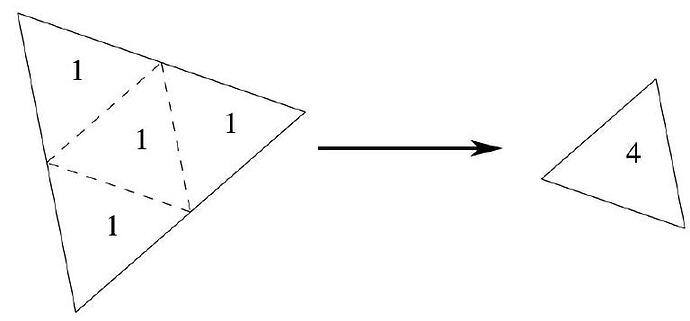
Consider a sheet of paper in the shape of an equilateral triangle creased along the dashed lines as in the figure below on the left. Folding over each of the three corners along the dashed lines creates a new object which is uniformly four layers thick, as in the figure below on the right. The number in each region indicates that region’s thickness (in layers of paper).
We have just seen one example of how a plane figure can be folded into an object with a uniform thickness. This problem asks you to produce several other examples. In each case, you may fold along any lines. The different parts that are folded may or may not be congruent. Assume that paper may be folded any number of times without tearing or becoming too thick to fold. If needed, you can use any of the following tools:
1- a magic ruler with which you can draw a line through any two given points and you can split any segment into as many equal parts as you wish; and
2- a right triangle tool with which you can drop perpendiculars from points to lines and erect perpendiculars to lines from points on them.
Given these rules:
(a) Show how to fold an equilateral triangle into an object with a uniform thickness of 3 layers.
(b) Show how to fold a 30^{\circ}-60^{\circ}-90^{\circ} triangle into an object with a uniform thickness of 3 layers.
(c) Show that every triangle can be folded into an object with a uniform thickness of 2020 layers.