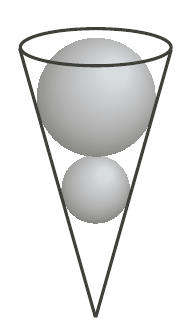
A cone is filled with water. Two solid spheres are placed in the cone as shown in the diagram and water spills out. (The spheres are touching each other, each sphere touches the cone all of the way around, and the top of the top sphere is level with the top of the cone.) The larger sphere has radius twice that of the smaller sphere. If the volume of the water remaining in the cone is 2016\pi, what is the radius of the smaller sphere? (The volume of a sphere with radius r is \displaystyle\frac43\pi r^3. The volume of a cone with radius r and height h is \displaystyle\frac13\pi r^2h.)
Answer Choices
A. 2\sqrt2
B. 6
C. 8
D. 6\sqrt2
E. 4\sqrt[3]2