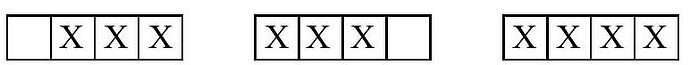Erin has an empty 1 \times 7 grid consisting of 1 \times 1 squares:
![]()
and follows the process below to construct a pattern:
- Place an \mathrm{X} in any empty square.
- If three or more consecutive squares each contain an \mathrm{X}, stop and do not add any more X's; otherwise, go to step (1) and continue the process.
For example, in a smaller 1 \times 4 grid, there are 3 different patterns that can be constructed:
(The last pattern may be obtained by placing X's, in order, in squares 1, 2, 4, and then 3.) By applying this process starting with the empy 1 \times 7 grid, how many different possible patterns can Erin construct?