Given x_{0} \in \mathbb{R}, f, g: \mathbb{R} \rightarrow \mathbb{R}, we define the non-redundant binary tree T\left(x_{0}, f, g\right) in the following way:
(a) The tree T initially consists of just x_{0} at height 0.
(b) Let v_{0}, \ldots, v_{k} be the vertices at height h. Then the vertices of height h+1 are added to T by: for i=0,1, \ldots, k, f\left(v_{i}\right) is added as a child of v_{i} if f\left(v_{i}\right) \notin T, and g\left(v_{i}\right) is added as a child of v_{i} if g\left(v_{i}\right) \notin T.
For example, if f(x)=x+1 and g(x)=x-1, then the first three layers of T(0, f, g) look like:
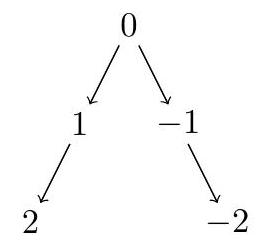
If f(x)=1024 x-2047\lfloor x / 2\rfloor and g(x)=2 x-3\lfloor x / 2\rfloor+2\lfloor x / 4\rfloor, then how many vertices are in T(2016, f, g)?