CMIMC 2018 Power Problem 1.1

Past Contests CMIMC CMIMC - 2018 Power
1

Let A=\left\{a_{1}, a_{2}, \ldots, a_{n}\right\} be a set of size n.

A permutation of A is a bijection \sigma: A \rightarrow A. In other words, a permutation is a way of rearranging the order of the elements in a set, so if you list out the elements of A in some order

a_{1}, \quad a_{2}, \quad \ldots, \quad a_{n}

you rearrange them to get

\sigma\left(a_{1}\right), \quad \sigma\left(a_{2}\right), \quad \ldots, \quad \sigma\left(a_{n}\right).

We can multiply two permutations \sigma_{1}, \sigma_{2} in the way we compose functions, i.e., \sigma_{1} \sigma_{2} is the permutation sending a_{i} to \sigma_{1}\left(\sigma_{2}\left(a_{i}\right)\right). Intuitively, this is equivalent to first rearranging the elements of A according to \sigma_{2} and then according to \sigma_{1}.

The product of two permutations is still a permutation. We denote \sigma^{k} to be \sigma \sigma \ldots \sigma, where \sigma is multiplied with itself k times. Let S_{A} denote the set of all permutations of the set A. We will use the abuse of notation S_{n} to denote the set of permutations of the set \{1,2, \ldots, n\}, i.e., S_{n}=S_{\{1,2, \ldots, n\}}.

We can represent a permutation in the following way:

\left(\begin{array}{ccccc} 1 & 2 & 3 & 4 & 5 \\ 3 & 1 & 5 & 4 & 2 \end{array}\right) \in S_{5}

which corresponds to the permutation sending 1 to 3, 2 to 1, 3 to 5, etc.

We call a permutation \sigma \in S_{n} a k-cycle or a cycle of length k if there are distinct integers a_{1}, a_{2}, \ldots, a_{k} such that

\sigma\left(a_{1}\right)=a_{2}, \quad \sigma\left(a_{2}\right)=a_{3}, \quad \ldots, \quad \sigma\left(a_{k}\right)=a_{1}

and \sigma(i)=i for all i \notin\left\{a_{1}, a_{2}, \ldots, a_{k}\right\}. In this case, we denote the permutation by \left(a_{1}, a_{2}, \ldots, a_{k}\right). For example, we now have two different notations for the permutation

(1,5,2)=\left(\begin{array}{lllll} 1 & 2 & 3 & 4 & 5 \\ 5 & 1 & 3 & 4 & 2 \end{array}\right).

  • Two cycles are called disjoint if none of their elements are the same. For example, (1,2,3) and (4,5,6) are disjoint, but (1,2,3) and (3,4,5) are not, since they share 3.

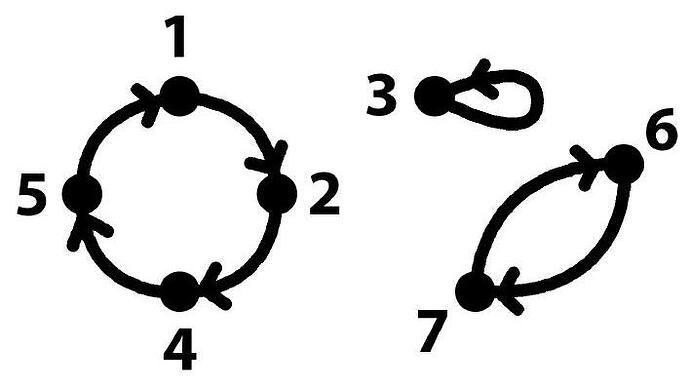
  • Every permutation can be written as the product of disjoint cycles. This representation is unique, up to rearranging the order in which we write them. One “proof by picture” of this fact is that you can always draw a diagram similar to this:

Image
Image708×396 20.4 KB

This picture illustrates the cycle decomposition of

\left(\begin{array}{lllllll} 1 & 2 & 3 & 4 & 5 & 6 & 7 \\ 2 & 4 & 3 & 5 & 1 & 7 & 6 \end{array}\right)=(1,2,4,5)(3)(6,7).

Above, writing adjacent cycles indicates multiplication of cycles (which is the same as composition).

The following parts are each worth 1 point.

(a) Give an expression for \left|S_{n}\right|, the number of elements in S_{n}, in terms of n.

(b) Let \sigma, \tau \in S_{6} be the permutations \sigma=(3,1,4,2) and \tau=(1,2,6,5). Compute \sigma \tau and write it as a product of disjoint cycles.

(c) Let \sigma and \tau be as above. Compute (\sigma \tau)^{2018}.