Consider a variant of this game called crazy concentration. This game is like concentration, except that in addition to the shuffled cards, a permutation \sigma \in S_{2 N} is fixed, but hidden from the player. This is called the mystery permutation. Then the following modification is made:
At the end of each turn, the player closes their eyes and the cards are rearranged according to the permutation \sigma, meaning the card in the i^{\text {th }} position from the left is placed in the \sigma(i)^{\text {th }} position instead.
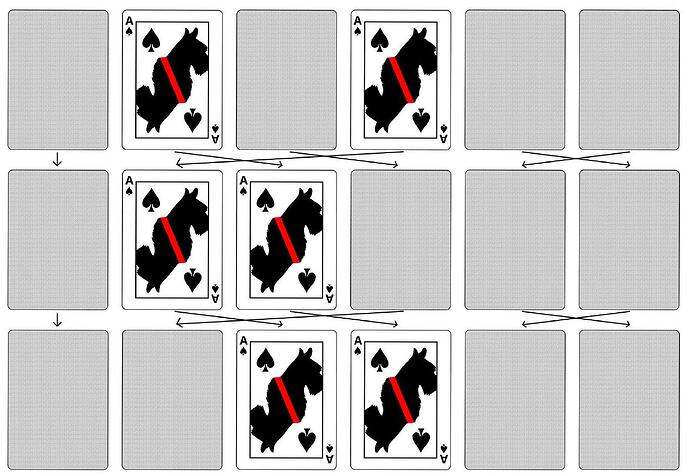
Note that cards that are flipped face-up remain face-up even during the rearrangement. The diagram below shows an excerpt of a game with 2 N=6, after which two cards have already been matched. The mystery permutation is given by
Show that if the mystery permutation is told to you, then you can guarantee finishing the game in at most 2 \mathrm{N} moves.