After years at sail, you and your crew have found the island that houses the great treasure of Scottybeard, the greatest pirate to ever sail the high seas. The island takes the shape of a unit square, and the treasure (which we treat as a single point) could be buried under any point on the island.
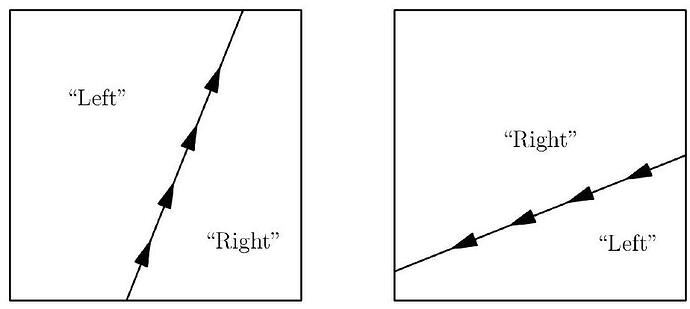
To assist you in finding his treasure, Scotty has left a peculiar instrument. To use this instrument, you may draw any directed line (possibly one that never hits the island!), and the instrument will tell you whether the treasure lies to the “left” or the “right” of the line. { }^{1}
However, Scotty also left a trap! If the instrument ever reports “left” three times in a row or “right” three times in a row, the island will suddenly sink into the sea, submerging the treasure forever and drowning you and your crew! You want to avoid this at all costs.
To minimize the amount of energy spent digging, you would like to narrow down the set of possible locations of the treasure to be as small as possible. However, Scotty left one last trick; you can only use the instrument 12 times before it breaks!
Devise an algorithm to use the instrument no more than 12 times that can never result in the island sinking and narrows the worst-case space of possible locations of the treasure to have as small an area as possible.
Scoring:
An algorithm that achieves a worst-case area of K will be awarded:
(where K_{\min } is the smallest possible worst-case area, which we are not disclosing to avoid giving anything away).
You may only submit one solution per problem. Please specify which bound you are trying to prove for your submission, or you may not be awarded points for that bound.
For an incorrect solution, partial points may be awarded for reasonable progress or achieving one of the weaker bounds. Partial points may be deducted for logical flaws or lack of rigor in proofs. To get full points, you must demonstrate that your algorithm never sinks the island, and always achieves at most your claimed worst-case area.
Where “left” or “right” is taken with respect to an observer walking along the line in its designated direction. There is also a probability zero chance the treasure is precisely on the line; this won’t affect anything, but for the sake of clarity let’s say the instrument reports “left” in this case.