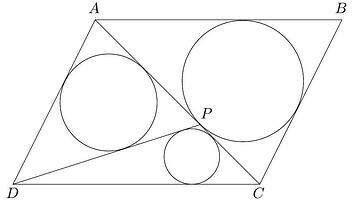
Let A B C D be a parallelogram. We draw in the diagonal A C. A circle is drawn inside \triangle A B C tangent to all three sides and touches side A C at a point P.
(a) Prove that D A+A P=D C+C P.
(b) Draw in the line D P. A circle of radius r_{1} is drawn inside \triangle D A P tangent to all three sides. A circle of radius r_{2} is drawn inside \triangle D C P tangent to all three sides. Prove that
\frac{r_{1}}{r_{2}}=\frac{A P}{P C}.
(c) Suppose D A+D C=3 A C and D A=D P. Let r_{1}, r_{2} be the two radii defined in (b). Determine the ratio r_{1} / r_{2}.