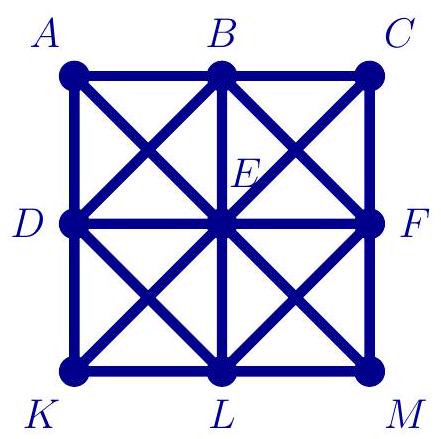
A 3 \times 3 grid of 9 dots labeled by A, B, C, D, E, F, K, L, and M is shown in the figure. There is one path connecting every pair of adjacent dots, either orthogonal (i.e. horizontal or vertical) or diagonal. A turtle walks on this grid, alternating between orthogonal and diagonal moves. One could describe any sequence of paths in terms of the letters A, \cdots, M. For example, A-B-F describes a sequence of two paths A B and B F.
What is the maximum number of paths the turtle could traverse, given that it does not traverse any path more than once?