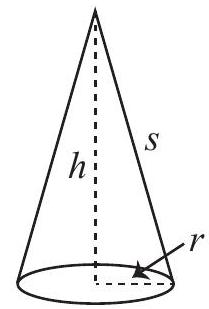
An unpainted cone has radius 3 \mathrm{~cm} and slant height 5 \mathrm{~cm}. The cone is placed in a container of paint. With the cone’s circular base resting flat on the bottom of the container, the depth of the paint in the container is 2 \mathrm{~cm}. When the cone is removed, its circular base and the lower portion of its lateral surface are covered in paint. The fraction of the total surface area of the cone that is
covered in paint can be written as \frac{p}{q} where p and q are positive integers with no common divisor larger than 1. What is the value of p+q ?
(The lateral surface of a cone is its external surface not including the circular base. A cone with radius r, height h, and slant height s has lateral surface area equal to \pi r s.)
Answer Choices
A. 59
B. 61
C. 63
D. 65
E. 67