A cylinder contains some water. A solid cone with the same height and half the radius of the cylinder is submerged into the water until the circular face of the cone lies flat on the circular base of the cylinder, as shown.
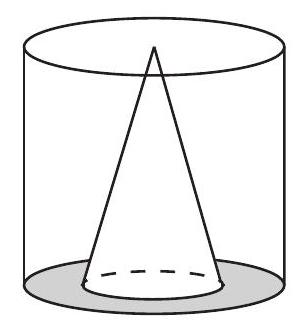
Once this is done, the depth of the water is half of the height of the cylinder. If the cone is then removed, the depth of the water will be what fraction of the height of the cylinder?
(The volume of a cylinder with radius r and height h is \pi r^{2} h and the volume of a cone with radius r and height h is \frac{1}{3} \pi r^{2} h.)
Answer Choices
A. \frac{3}{16}
B. \frac{41}{96}
C. \frac{5}{16}
D. \frac{3}{8}
E. \frac{7}{16}