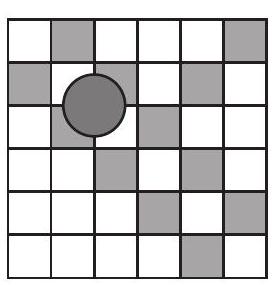
Nate has a grid made of shaded and unshaded 2 \mathrm{~cm} by 2 \mathrm{~cm} squares, as shown. He randomly places a circle with a diameter of 3 \mathrm{~cm} on the board so that the centre of the circle is at the meeting point of four squares. What is the probability that he places the disk so that it is touching an equal number of shaded and unshaded squares?
Answer Choices
A. \frac{13}{25}
B. \frac{17}{25}
C. \frac{11}{25}
D. \frac{21}{25}
E. \frac{3}{5}