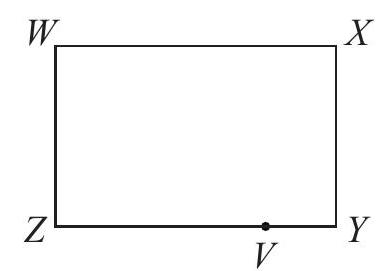
Rectangle W X Y Z has W X=4, W Z=3, and Z V=3. The rectangle is curled without overlapping into a cylinder so that sides W Z and X Y touch each other. In other words, W touches X and Z touches Y. The shortest distance from W to V through the inside of the cylinder can be written in the form \sqrt{\frac{a+b \pi^{2}}{c \pi^{2}}} where
a, b and c are positive integers. The smallest possible value of a+b+c is
Answer Choices
A. 12
B. 26
C. 18
D. 19
E. 36