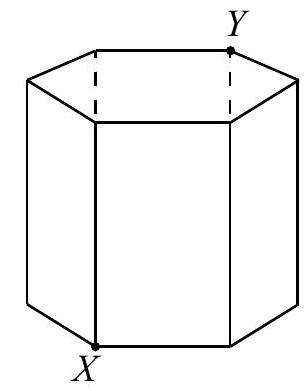
A hexagonal prism has a height of 165 \mathrm{~cm}. Its two hexagonal faces are regular hexagons with sides of length 30 \mathrm{~cm}. Its other six faces are rectangles. A fly and an ant start at point X on the bottom face and travel to point Y on the top face. The fly flies directly along the shortest route through the prism. The ant crawls around the outside of the prism along a path of constant slope so that it winds around the prism exactly n+\frac{1}{2} times, for some positive integer n. The distance crawled by the ant is more than 20 times the distance flown by the fly. What is the smallest possible value of n ?