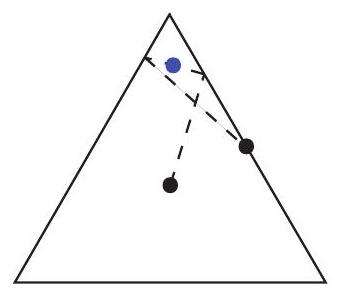
Consider a pool table with the shape of an equilateral triangle. A ball of negligible size is initially placed at the center of the table. After it has been hit, it will keep moving in the direction it was hit towards and bounce off any edges with perfect symmetry. If it eventually reaches the midpoint of any edge, we mark the midpoint of the entire route that the ball has travelled through. Repeating this experiment, how many points can we mark at most?