On an infinite triangular lattice, there is a single atom at a lattice point. We allow for four operations as illustrated in Figure 1. In words, one could take an existing atom, split it into three atoms, and place them at adjacent lattice points in one of the two displayed fashions (a “split”). One could also reverse the process, i.e. taking three existing atoms in the displayed configurations, and merge them into a single atom at the center (a “merge”).
Figure 1: See Individual Finals Problems document for diagram.
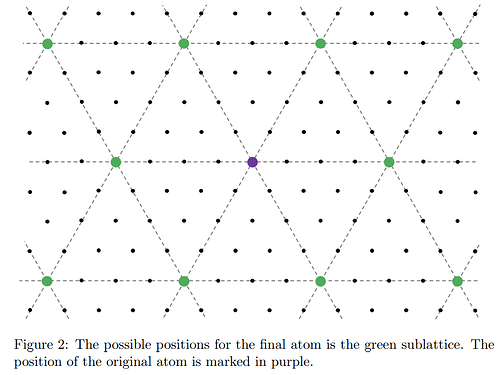
Assume that, after finitely many operations, there is again only a single atom remaining on the lattice. Show that this is possible if and only if the final atom is contained in the sublattice implied by Figure 2.
Figure 2: See Individual Finals Problems document for diagram.