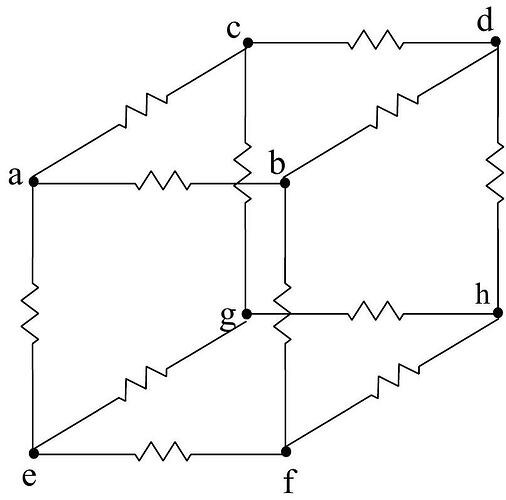
A group of 12 resistors is arranged along the edges of a cube as shown in the diagram below. The vertices of the cube are labeled a-h.
a. (13 pts) The resistance between each pair of vertices is as follows:
R_{a b}=R_{a c}=R_{a e}=3.0 \Omega
R_{c g}=R_{e f}=R_{b d}=8.0 \Omega
R_{c d}=R_{b f}=R_{e g}=12.0 \Omega
R_{d h}=R_{f h}=R_{g h}=1.0 \Omega
What is the equivalent resistance between points a and h ?
b. (12 pts) The three 12.0 \Omega resistors are replaced by identical capacitors. C_{c d}=C_{b f}=C_{e g}= 15.0 \mu \mathrm{F}. A 12.0 \mathrm{~V} battery is attached across points a and h and the circuit is allowed to operate for a long period of time. What is the charge ( Q_{c d}, Q_{b f}, Q_{e g} ) on each capacitor after this long period of time?