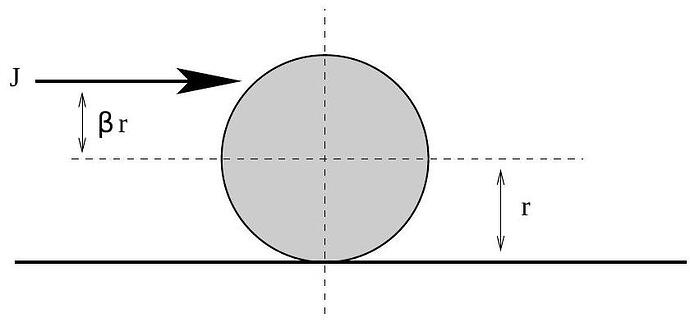
A uniform pool ball of radius r and mass m begins at rest on a pool table. The ball is given a horizontal impulse J of fixed magnitude at a distance \beta r above its center, where -1 \leq \beta \leq 1. The coefficient of kinetic friction between the ball and the pool table is \mu. You may assume the ball and the table are perfectly rigid. Ignore effects due to deformation. (The moment of inertia about the center of mass of a solid sphere of mass m and radius r is I_{c m}=\frac{2}{5} m r^{2}.)
a. Find an expression for the final speed of the ball as a function of J, m, and \beta.
b. For what value of \beta does the ball immediately begin to roll without slipping, regardless of the value of \mu?