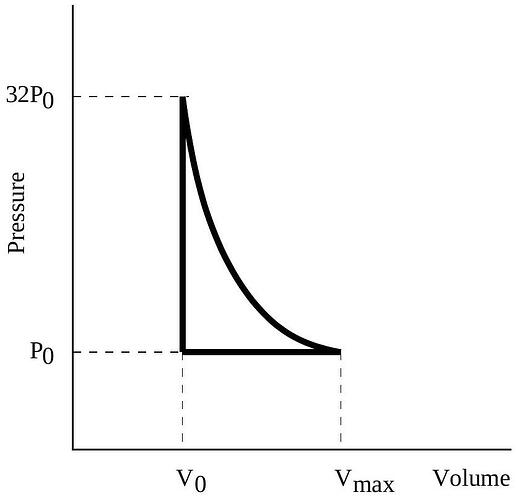
A simple heat engine consists of a moveable piston in a cylinder filled with an ideal monatomic gas. Initially the gas in the cylinder is at a pressure P_{0} and volume V_{0}. The gas is slowly heated at constant volume. Once the pressure reaches 32 P_{0} the piston is released, allowing the gas to expand so that no heat either enters or escapes the gas as the piston moves. Once the pressure has returned to P_{0} the outside of the cylinder is cooled back to the original temperature, keeping the pressure constant. For the monatomic ideal gas you should assume that the molar heat capacity at constant volume is given by C_{V}=\frac{3}{2} R, where R is the ideal gas constant. You may express your answers in fractional form or as decimals. If you choose decimals, keep three significant figures in your calculations. The diagram below is not necessarily drawn to scale.
a. Let V_{\max } be the maximum volume achieved by the gas during the cycle. What is V_{\max } in terms of V_{0} ? If you are unable to solve this part of the problem, you may express your answers to the remaining parts in terms of V_{\max } without further loss of points.
b. In terms of P_{0} and V_{0} determine the heat added to the gas during a complete cycle.
c. In terms of P_{0} and V_{0} determine the heat removed from the gas during a complete cycle.
d. What is the efficiency of this cycle?