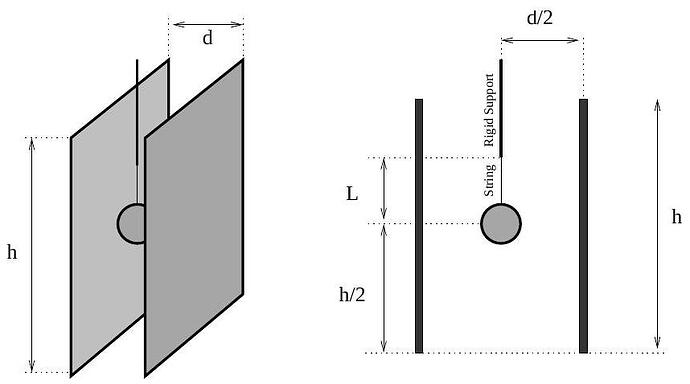
Consider a parallel plate capacitor with the plates vertical. The plates of the capacitor are rigidly supported in place. The distance between the plates is d. The plates have height h and area A \gg d^{2}. Assume throughout this problem that the force of air resistance may be neglected; however, the force of gravity cannot be neglected. Neglect any edge effects as well as any magnetic effects.
a. A small metal ball with a mass M and a charge q is suspended from a string of length L that is tied to a rigid support. When the capacitor is not charged, the metal ball is located at the center of the capacitor- at a distance d / 2 from both plates and at a height h / 2 above the bottom edge of the plates. If instead a constant potential difference V_{0} is applied across the plates, the string will make an angle \theta_{0} to the vertical when the metal ball is in equilibrium.
i. Determine \theta_{0} in terms of the given quantities and fundamental constants.
ii. The metal ball is then lifted until it makes an angle \theta to the vertical where \theta is only slightly greater than \theta_{0}. The metal ball is then released from rest. Show that the resulting motion is simple harmonic motion and find the period of the oscillations in terms of the given quantities and fundamental constants.
iii. When the ball is at rest in the equilibrium position \theta_{0}, the string is cut. What is the maximum value for V_{0} so that the ball will not hit one of the plates before exiting? Express your answer in terms of the given quantities and fundamental constants.
b. Suppose instead that the ball of mass M and charge q is released from rest at a point halfway between the plates at a time t=0. Now, an AC potential difference V(t)=V_{0} \sin \omega t is also placed across the capacitor. The ball may hit one of the plates before it falls (under the influence of gravity) out of the region between the plates. If V_{0} is sufficiently large, this will only occur for some range of angular frequencies \omega_{\min }<\omega<\omega_{\max }. You may assume that \omega_{\min } \ll \sqrt{g / h} and \omega_{\max } \gg \sqrt{g / h}. Making these assumptions, find expressions for \omega_{\min } and \omega_{\max } in terms of the given quantities and/or fundamental constants.
c. Assume that the region between the plates is not quite a vacuum, but instead humid air with a uniform resistivity \rho. Ignore any effects because of the motion of the ball, and assume that the humid air doesn’t change the capacitance of the original system.
i. Determine the resistance between the plates.
ii. If the plates are originally charged to a constant potential source V_{0}, and then the potential is removed, how much time is required for the potential difference between the plates to decrease to a value of V_{0} / e, where \ln e=1 ?
iii. If the plates are instead connected to an AC potential source so that the potential difference across the plates is V_{0} \sin \omega t, determine the amplitude I_{0} of the alternating current through the potential source.