A hollow cylinder has length l, radius r, and thickness d, where l \gg r \gg d, and is made of a material with resistivity \rho. A time-varying current I flows through the cylinder in the tangential direction. Assume the current is always uniformly distributed along the length of the cylinder. The cylinder is fixed so that it cannot move; assume that there are no externally generated magnetic fields during the time considered for the problems below.
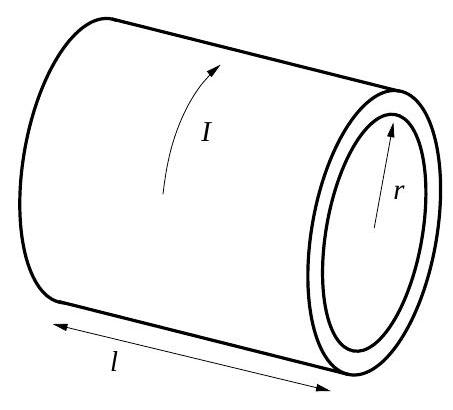
a. What is the magnetic field strength B inside the cylinder in terms of I, the dimensions of the cylinder, and fundamental constants?
b. Relate the emf \mathcal{E} developed along the circumference of the cylinder to the rate of change of the current \frac{d I}{d t}, the dimensions of the cylinder, and fundamental constants.
c. Relate \mathcal{E} to the current I, the resistivity \rho, and the dimensions of the cylinder.
d. The current at t=0 is I_{0}. What is the current I(t) for t>0 ?