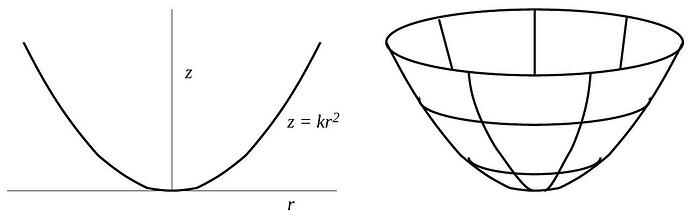
A particle is constrained to move on the inner surface of a frictionless parabolic bowl whose crosssection has equation z=k r^{2}. The particle begins at a height z_{0} above the bottom of the bowl with a horizontal velocity v_{0} along the surface of the bowl. The acceleration due to gravity is g.
a. For a particular value of horizontal velocity v_{0}, which we will name v_{h}, the particle moves in a horizontal circle. What is v_{h} in terms of g, z_{0}, and/or k ?
b. Suppose that the initial horizontal velocity is now v_{0}>v_{h}. What is the maximum height reached by the particle, in terms of v_{0}, z_{0}, g and/or k ?
c. Suppose that the particle now begins at a height z_{0} above the bottom of the bowl with an initial velocity v_{0}=0.
i. Assuming that z_{0} is small enough so that the motion can be approximated as simple harmonic, find the period of the motion in terms any or all of the mass of the particle m, g, z_{0}, and/or k.
ii. Assuming that z_{0} is not small, will the actual period of motion be greater than, less than, or equal to your simple harmonic approximation above? (You need not calculate the new value explicitly, but you should show some work to defend your answer.)