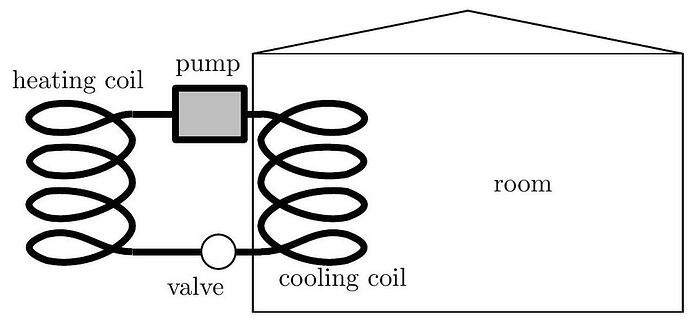
A room air conditioner is modeled as a heat engine run in reverse: an amount of heat Q_{L} is absorbed from the room at a temperature T_{L} into cooling coils containing a working gas; this gas is compressed adiabatically to a temperature T_{H}; the gas is compressed isothermally in a coil outside the house, giving off an amount of heat Q_{H}; the gas expands adiabatically back to a temperature T_{L}; and the cycle repeats. An amount of energy W is input into the system every cycle through an electric pump. This model describes the air conditioner with the best possible efficiency.
Assume that the outside air temperature is T_{H} and the inside air temperature is T_{L}. The air-conditioner unit consumes electric power P. Assume that the air is sufficiently dry so that no condensation of water occurs in the cooling coils of the air conditioner. Water boils at 373 \mathrm{~K} and freezes at 273 \mathrm{~K} at normal atmospheric pressure.
a. Derive an expression for the maximum rate at which heat is removed from the room in terms of the air temperatures T_{H}, T_{L}, and the power consumed by the air conditioner P. Your derivation must refer to the entropy changes that occur in a Carnot cycle in order to receive full marks for this part.
b. The room is insulated, but heat still passes into the room at a rate R=k \Delta T, where \Delta T is the temperature difference between the inside and the outside of the room and k is a constant. Find the coldest possible temperature of the room in terms of T_{H}, k, and P.
c. A typical room has a value of k=173 \mathrm{~W} /{ }^{\circ} \mathrm{C}. If the outside temperature is 40^{\circ} \mathrm{C}, what minimum power should the air conditioner have to get the inside temperature down to 25^{\circ} \mathrm{C}?